

Algebra is one of the most complex and most interesting parts of Mathematics. Yes, hard when you don’t understand it and super interesting when you realize how easy it is. Algebra questions involve numbers, letters, and symbols to find hidden values. Algebra can help determine values that can change.
Since the GSCE exams are just around the corner, we felt the need to prepare the students for Algebra. Therefore, we will compile a list of 10 solved Algebra problems and explanations below to help you practice.
But before that, let’s go through a few more details related to algebra and its techniques briefly!
There are three main techniques for solving Algebra problems: KS2, KS3, and KS4. In KS2, we simplify and write the expressions and solve and substitute the equations.
In KS3 questions, we learn and practice writing the basic linear equations and algebraic expressions.
In KS4, we deal with more complex Algebraic expressions, including the system of linear equations and quadratic equations. In short, KS4 is the most complicated and advanced technique for solving Algebraic problems.
Below, you will find solved examples involving all these three techniques. But first, let us see the basic methods of solving Algebraic problems.
The first to solve an Algebraic question is to determine and identify what you need to find. For that, you need to go through the question carefully and thoroughly. Here are a few examples of what algebraic problems can ask you to find:
Another thing you need to keep in mind while solving algebraic expressions is that you always need to apply the BODMAS or BIDMAS rule. The full form of these terms is Brackets, Indice, Division, Multiplication, Addition, and Subtraction.
According to this rule, you need to solve the equation in the same sequence and order as mentioned above, i.e., First, solve the brackets/indices, then perform division, etc.
We simplify, substitute, and solve equations in the KS2 type questions as we briefly mentioned above. Like we promised, here are a few solved examples with explanations:
We have two products; a chocolate bar and a drink. The chocolate costs c dollars, and the drink costs d dollars. What will be the algebraic equation if we want to find the cost of 2 chocolates and 2 drinks?
Answer: 2c + 2d
Explanation: Since we need to find the cost of 2 drinks and 2 chocolates, their lots will be 2c and 2d respectively.

4m + 5 + 2m – 1: Simplify this equation.
Answer: 6m + 4
Explanation: First, you need to organize the equation in order, i.e., 4m + 2m + 5 -1.
Now, 4m + 2m will be 6m, and 5 – 1 will be 4. Hence, 6m + 4.

In the KS3 Algebraic equations, we use the following techniques and steps:
Now, here are a few solved examples of the KS3 Algebra questions, along with their explanations.
Here is a pyramid with 3 values given in boxes, and you need to find the box’s value above. You will need to add two more adjacent blocks to find the answer. What expression should be in the box above?
Answer: 12a – b
Explanation:
Josh is a window cleaner, and he calculates the charging amount of his customers using this formula:
Charge = £20 + 4n
In this formula, n is the number of windows in a house. So, how much will Josh charge if a house has 7 windows?
Answer: £48
Explanation: Since n is the number of windows, we put n = 7. So, 20 + 4 x 7 = 48. Hence, Charge = £48.

We have a rectangle with an area of 4x – 6. What will be the length and width of this rectangle?
Answer: 2 and 2x -3
Explanation: We solved this problem through factorization.
= 4x – 6
= 2(2x -3)
This means the length and width are 2 and 2x – 3, respectively.

For changing Celsius to degrees Fahrenheit, the formula is:
F = 9C/5 + 32
How can you make c the subject of this formula?
Answer: C = 5 (F – 32) / 9
Explanation:
F = 9C/5 + 32
Now, subtract 32.
F – 32 = 9C / 5
Now, multiply by 5.
5 (F – 32) = 9c
Now, divide by 9.
5 (F – 32) / 9 = C

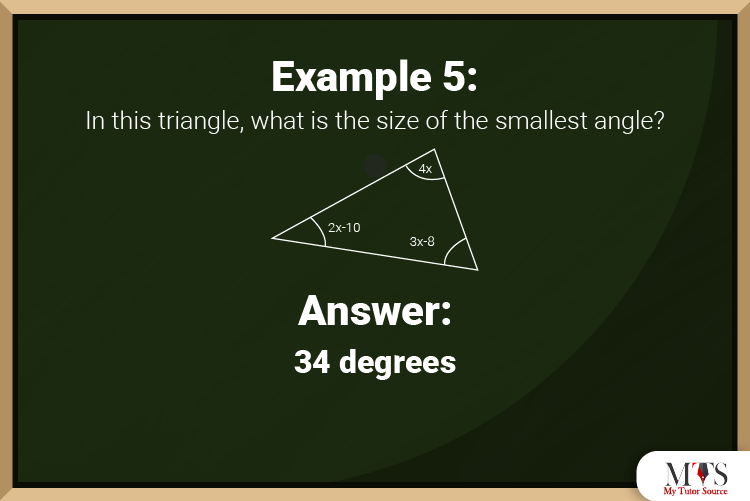
In this triangle, what is the size of the smallest angle?
Answer: 34 degrees
Explanation: A triangle has angles with a sum of 180 degrees, right? Hence, we can write:
4x + 2x – 10 + 3x – 8 = 180
Now, we will solve this equation:
9x – 18 = 180
Now, we add 18
9x = 198
Now, we divide it by 9
x = 22 degrees
Now, the angles are:
4 x 22 = 88 degrees
2 x 22 – 10 = 34 degrees
3 x 22 – 8 = 58 degrees
Hence, the smallest angle is 34 degrees.
Kate’s dad is 4 times older than her. After 14 years, Kate’s dad will be twice her age. What is the sum of kate and her dad’s age right now?
Answer: 35
Explanation: To solve this word problem, we will need to write an equation with the given variables and values.
Suppose Kate’s age is x, and her dad’s age is 4x. After 14 years, Kate’s age will be x + 14, and her dad’s age will be 4x + 14.
Now, we know that Kate’s dad is 2 times her age, our equation will be:
4x + 14 = 2(x + 14)
Now, we will solve this equation.
4x + 14 = 2(x + 14)
Now, we will expand the brackets.
4x + 14 = 2x + 28
Now, we will subtract 2x.
2x + 14 = 28
Now, we will subtract 14.
2x = 14
X = 7
Hence, kate is currently 7 years old, and her dad is 28 years old. The sum of their age will be 35.

KS4 is the most advanced and complicated type of algebraic problem. Here is the list of topics and techniques included in it:
Here are a few solved examples of KS4 algebraic questions:
Find the volume of this cuboid with an x expression:
Answer: 30×3 – 49×2 + 4x + 3
Explanation: Since the volume of a cuboid is Length x Width x Height
Volume = (5x + 1)(2x – 3)(3x – 1)
Volume = (10x2 + 2x – 15x – 3)(3x – 1)
Volume = (10x2 – 13x – 3)(3x – 1)
Volume = 30x3 – 39x2 – 9x – 10x2 +13x + 3
Volume = 30x3 – 49x2 + 4x + 3

The area of this given triangle is 24 cm2, what will be its perimeter?
Answer: 24 cm
Explanation: The formula to find the area of a triangle is:
Area = ½ x b x h.
Now, we will fill it in.
24 = ½ x 6 x (3x – 1)
Simplify
24 = 3(3x -1)
Multiply the brackets
24 = 9x – 3
Add 3
27 = 9x
Divide by 9
X = 3
Now that x = 3, the side lengths of the triangle will be 6 cm, 8 cm, and 10 cm.
Perimeter = 6 + 8 + 10 = 24 cm.

X + 2 – 15/x = 0
Solve this equation?
Answer: x = -5 04 x = 3
Explanation:
x + 2 – 15/x = 0
Multiply b x
x2 + 2x – 15 = 0
Factorize
(x + 5)(x – 3) = 0
Solve
x = 15 or x = 3

What will be the minimum value of the function f(x) = x2 + 4x + 5?
Answer: 1
Explanation: To find the minimum value of this function, first you will have to complete the square.
f(x) = x2 + 4x + 5
f(x) = (x + 2)2 – 4 + 5
f(x) = (x + 2)2 + 1
Hence, the minimum value is 1.

I hope our list of 10 solved algebraic questions helps you prepare for your GSCE exams. We tried to cover almost all types of algebraic expressions and equations. Now it’s your turn to practice these questions, understand the methods and concepts, and ace your exam!
If you still have questions or confusion, you can always contact us and ask for a professional Mathematics tutor to clear your concepts. Your tutor is only a click away!