What is an area?
The space that is occupied by a flat shape or the surface of an object. The standard unit of measurement is mostly either ㎡ or cm2. We are going to discuss the Area of triangles here.
What is a triangle?
Triangle is the most powerful geometry, which is a closed two-dimensional shape having three (3) sides. There are different types of triangles based on sides and based on angles. There are three different types of triangles based on sides; Equilateral,
Isosceles, and Scalene. There are three different types of triangles based on
angles; Right, Acute and Obtuse.
Area of triangle:
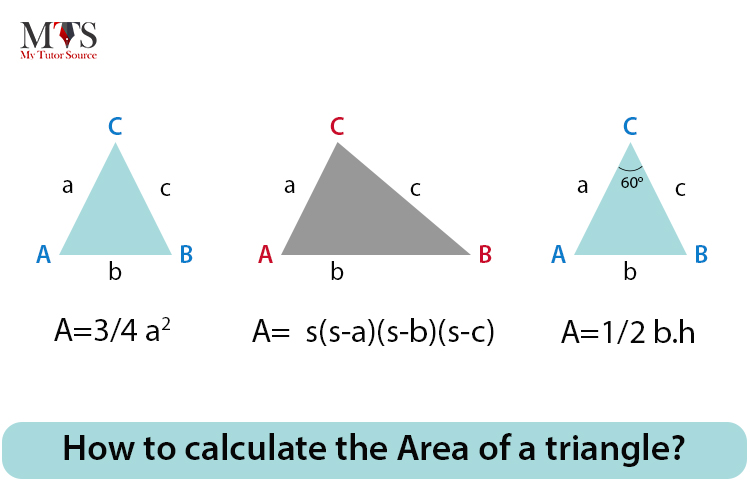
The area of a triangle is the region enclosed by the three sides of any kind of triangle; the space occupied by it.. In mathematical terms, Area of a triangle is 12bh. Here b means base, and h means height. If one knows that the Area of a rectangle is b x h, then one can understand that the diagonal of a rectangle makes two different triangles which basically drives the formula for the Area of a triangle. Moreover, the base and height of a triangle are perpendicular to each other, and as mentioned before, in finding areas of the triangles, the unit of Area is measured in square units ㎡ or cm2.
For example:
What is the area of a triangle, with base b = 4cm and height h = 5cm?
By applying the formula:
Area of a triangle =12bh
= 124cm5cm
= 1220 cm2
= 10 cm2
Equilateral triangles and Area of an Equilateral Triangle:
The triangles in which the length of all the sides are equal are called equilateral triangles. In order to find the area of an equilateral triangle, we need to know the formula and since the only information that is always given to us in equilateral triangles is the measurement of the sides of the triangle. The formula for finding the area of the equilateral triangle is 34a2. The formula can be written as Area of the equilateral triangle = 0.433 a2. Here, a means the sides of the equilateral triangles.
For example:
What is the area of the equilateral triangle with sides 4cm?
By applying the formula:
Area of a triangle =34a2
= 344cm2
= 3416 cm2
= 6.928cm2
A Right Angled Triangle and Area of a Right angled triangle:
The triangle, which has one side with an angle of 90° and the other two sides collectively make a total angle of 90°. In this triangle, sometimes height is given, but often one has to find out the height by using Pythagoras theorem, that is a2+b2= c2 showing that the square of the longest side “c” is equal to the sum of the squares of the other two sides, here a, b and c are sides of the triangle. However, since, in order to find the height, we will draw the line, which will make the base of the triangle half. Area of a right-angled triangle = 12bh.
For example,
The base of a triangle is 24cm and the other sides are 20cm, find the area of the right angled triangle?
By applying the formula:
Area of a right-angled triangle = 12bh.
In order to apply Pythagoras theorem, by drawing the line between triangle, the base will be divided into two different parts so now b would be equal to 242= 12.
In order to find the height, we have to apply Pythagoras theorem:
a2+b2= c2
(a)2+(12)2= (20)2
(a)2+ 144 = 400
(a)2= 400 – 144
(a)2= 256
(a)2= 256
a = 16 cm
So now we have the height and will be able to calculate the area of the right angled triangle:
Area of a right angled triangle = 12bh
= 121216
= 12192
= 96 cm2
An Isosceles Triangle and Area of an Isosceles Triangle:
The triangle which has length of two sides equal is called an isosceles triangle. The formula for finding the area of an isosceles triangle is 12bh. It is done in the same way as of the right angle triangle. First we have to find the height which in the above mentioned example was 16 cm. However in finding the area of an isosceles triangle the base will remain 24 cm without dividing it by half.
For Example:
The base of a triangle is 24cm and the other sides are 20cm, height is 16cm. Find the area of the isosceles triangle?
By applying the formula:
Area of an isosceles triangle = 12bh.
= 1224cm16cm
= 12384 cm2
= 192 cm2
If you are finding this topic hard or maths in general then you can get help from a Private
Maths tutor.
A Scalene triangle and area of a scalene triangle:
A triangle in which the length of all sides are different is called a scalene triangle. In order to find the area of a scalene triangle we use a totally different formula; Heron’s formula. Heron’s formula = s(s-a)(s-b)(s-c)which has two important steps. First, we need to know how to calculate the perimeter of a triangle and then how to calculate the area using the whole formula. In the formula s denotes the perimeter of a triangle divided by two and a,b, and c denotes the sides of the triangle.
The perimeter of a triangle is the sum of all its three sides.
Perimeter of a triangle = a + b + c
However in the heron’s formula the S denotes Perimeter divided by two (2). S= P/2. It can also be written as Semi-Perimeter.
For example:
The sides of a triangle are 9, 11, and 16. Find the area of the scalene triangle?
By applying the formula,
First we need to find the s “Semi perimeter”
Semi perimeter = s = a+b+c2
= 9+11+162
= 362
= 18
Heron’s formula = s(s-a)(s-b)(s-c)
=18(18-9)(18-11)(18-16)
=18(9)(7)(2)
=18(126)
=18(126)
=2268
=47.6235 cm2
Area of a triangle with two sides and an included angle:
How to Find the Area of a triangle when we know the two sides of a triangle and an angle included between them.
For example, let’s take a triangle XYZ, whose vertex angles are ∠X, ∠Y, and ∠Z, and sides are x,y, and z. Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by:
Area (∆XYZ) = 12yz sin X
Area (∆XYZ) =12 xy sin Z
Area (∆XYZ) = 12zx sin Y
For example:
If in a triangle with the angle of 30°, the two sides a and c are 8 and 7 cm respectively. Find the area of the triangle?
By applying the formula:
Area (∆ABC) =12 ac sin B
Area (∆ABC) =12 8cm 7cm sin (30°)
Area (∆ABC) =12 56 cm2 12
Area (∆ABC) = 14cm2
Find Top Tutors in Your Area
Find A Tutor