

Do you have an assignment from school that requires you to find out the area of various cylinders but you don’t know what to do? Well, here is how to find the volume of a cylinder:
The cylinder can be defined as a three-dimensional (3D) shape with a circular base. You can also consider a cylinder as a set of circular or round disks that are stacked over each other. Now, with this definition in mind, consider a situation where you’ve to calculate how much sugar you can accommodate in a cylindrical box.
In other words, you’ve to find out the volume or the capacity of that cylindrical box. The capacity of a certain cylindrical box is equal to the volume of the cylinder that is involved. Therefore, the volume of a three-dimensional (3D) shape is considered equal to the amount of space that the said shape occupies.
Like we have mentioned above, a cylinder can be considered a set of multiple congruent or circular disks that are stacked over one another. So, to calculate the space that the cylinder occupies, you have to calculate the space that each disk in that stack occupies, and then add them up. In other words, the volume of cylinder can be found out by the product of the area of height and base.
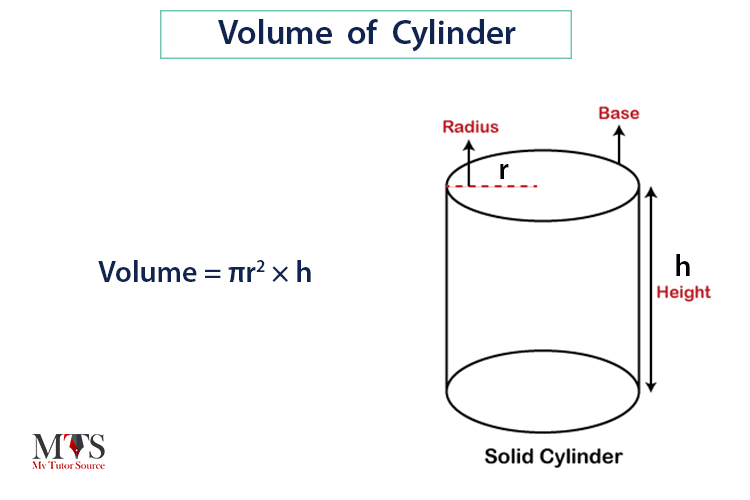
For a cylinder whose base radius is ‘r’, and height is ‘h’, its volume will be base times the height.
So, the volume will be ‘(area of base) × height of the cylinder’
Since the base of a cylinder is a circle, the volume can be written as:
Volume = πr2 × h
Hence, the volume of a cylinder = πr2h cubic units.
where:
Π (Pi) = 3.142
r = radius of the base of cylinder
h = height of cylinder
And this is the formula of volume of rod or cylinder!
Example
Find out the volume of a cylinder with a height of 20 cm and a base radius of 14 cm. Use pi as 22/7.
Solution:
You are given the following measurements:
Height = 20 cm
radius = 14 cm
You are required to find:
Volume of cylinder = ?
You already know the formula for the volume of a cylinder:
V (Volume) = πr2h cubic units
So, apply the given measurements in the formula written above:
V=(22/7) × 14 × 14 × 20
V= 12320 cm³
Hence, the correct volume of the cylinder is 12320 cm³.
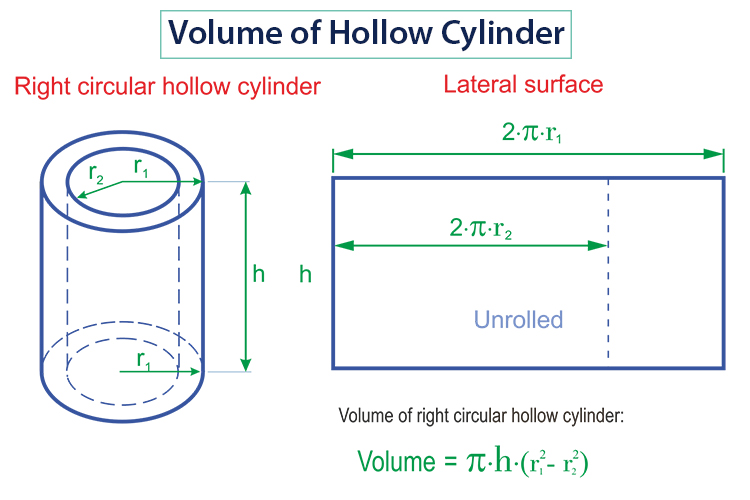
If you’ve a hollow cylinder, you’ll have to measure two radii; one for the inner circle and one for the outer one that is created by the base of the hollow cylinder.
Suppose, the two radii of a hollow cylinder are r1 and r2, respectively, and ‘h’ is the height of the hollow cylinder, then the equation for the volume of hollow cylinder can be written as:
V = πh(r1² – r2²)
Related read: https://mytutorsource.com/blog/types-of-angles/
But what about when you’ve a partially filled cylinder, for instance, a horizontal cylindrical tank that is partly filled with oil. You can use the formula given above to find out the volume of cylinder which will give you the maximum capacity of that cylinder. However, you’ll have to find out the volume of the oil in the tank given the depth of the oil.
You can easily find that out by using the method involved in the measurement of volume of a horizontal cylindrical segment.
In an oblique cylinder the top center isn’t over the center point of the base. Surprisingly, it turns out that the formula to find out the surface volume of a cylinder works the same for these. However, you must use the perpendicular height in the case of oblique cylinders. The perpendicular height is the vertical line to the left.
Sometimes you’ve to calculate both surface areas and volumes of cylinder. Now you already know the formula for the latter, so let’s study the former. The number of square units that are needed to cover the surface of a cylinder is the surface area of that particular cylinder. The formula for the surface area is:
A = 2πr² + 2πrh
You can also write this formula as:
A = 2πr(h+r)
If you require an answer in litres, you can convert the volume in cubic centimetres to litres by using the following conversion:
1 Litre = 1000 cm³ or cubic cm
For instance, if a cylinder’s volume is 12 litres, you can write its volume as:
12 × 1000 cm³ = 12,000 cm³
Always keep in mind that the height of the cylinder and the radius of the base must be in the same units. If you’ve to solve a problem that enlists them in different units, you must convert them before you start solving the question. The result of the product of base and height AKA the volume will be in those cubic units.
Thus, for instance, if the height of a cylinder and the radius of its base are both in centimeters, then the volume of that cylinder will be in cubic centimeters (cm³).
And that is it. You’ve all the formulae that you need for school to ace your maths exam. No matter what type of cylinder you have, whether it is oblique or hollow, or if it is partially filled, you know what formula to use for what situation. So, regardless of what you are required to calculate for an exam, be it surface area or volume of cylinder, you’ve got it, as long as you remember your formula!