
![What are Polygons? [Types, Shapes, Formulas and Examples]](https://mytutorsource.com/assets/admin/blogimages/1649058608.What-are-Polygons.png)
Learning to design interior and exterior angles of polygons is one of the most daunting tasks for students during geometry class: teachers and private math tutors say so. Polygon is a 2D (two-dimensional) geometric figure constructed with straight lines having a finite number of sides. Triangle with three sides is the most common example of a polygon. However, there are plenty of common and uncommon polygon shapes we see and experience without even knowing.
In this blog post, you will learn everything about polygons, such as their mathematical definition, shapes, types, properties, real-life examples, other examples, and many more things in detail. Before we start learning, here is some interesting information for you. Polygon comes from the Greek language, in which Poly means ‘many’ and -gon means ‘angle.’
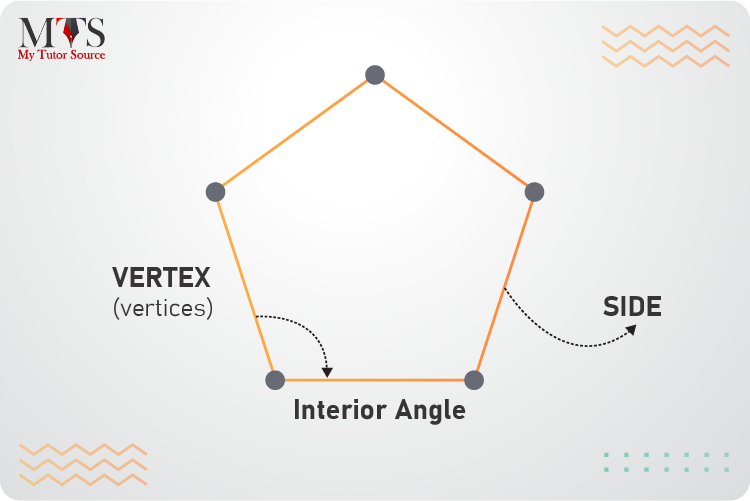
Any close two-dimensional shape or plane figure formed with straight line segments is known as a polygon. Open shapes or curved ones don’t make a polygon. It’s a combination of two words, which means ‘many sides .’A polygon comprises many straight-line segments, and the points where these line segments meet are called corners or vertices, making an angle. Moreover, the line segments are called edges or sides. The sides of polygons are not limited, and they could have 3 sides, 11 sides, 44 sides, or more. It can have as many sides as needed. However, the name of the polygon will surely change or differ.
Following are the most common geometrical shapes of a polygon. These all are the perfect shapes and examples of a polygon. However, the number of sides vary, as given below:
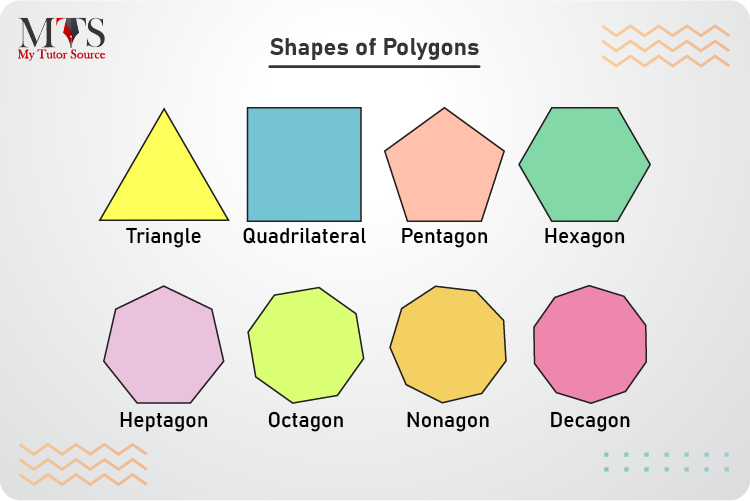
| Shapes of Polygon | Number of Sides |
| Rectangle | 4 |
| Triangle or Trigon | 3 |
| Square | 4 |
| Quadrilateral or Tetragon | 4 |
| Pentagon | 5 |
| Octagon | 8 |
| Nonagon or Enneagon | 9 |
| Hexagon | 6 |
| Heptagon or Septagon | 7 |
| Decagon | 10 |
| n-gon | n sides |
| Hendecagon or Undecagon | 11 |
Polygons are classified into different types depending on the number of sides and angles. Following are the types of polygons with details and examples:

A polygon is regular if all sides and interior angles are equal.
For Example: equilateral triangle, square, etc.
A polygon is of irregular type if its sides and interior angles are different in measure. They are primarily in the shape of a pentagon, hexagon, or a different shape compared to the regular polygon.
For Example: a rectangle, scalene triangle, kite, etc.
A polygon with inward and outward vertices, one or more interior angles of more than 180 degrees, is a concave polygon. They have at least four sides.
Hint: concave has a cave in it means its internal angle will always be greater than 180°.
A polygon will be of convex type if all internal angles are less than 180 degrees. Its vertices are mostly outwards and are exactly opposite of the concave polygon.
Any polygon with only one boundary is called a simple polygon. Its lines do not cross over each other.
For Example: a pentagon
A polygon whose sides cross over or intersect each other is called a complex polygon. Such polygons are also known as self-intersecting polygons.
Note: a few polygon rules do not work on the complex polygon.
For Example: antiparallelogram, star, etc.
Mainly the angles of the polygons are categorized into two types:
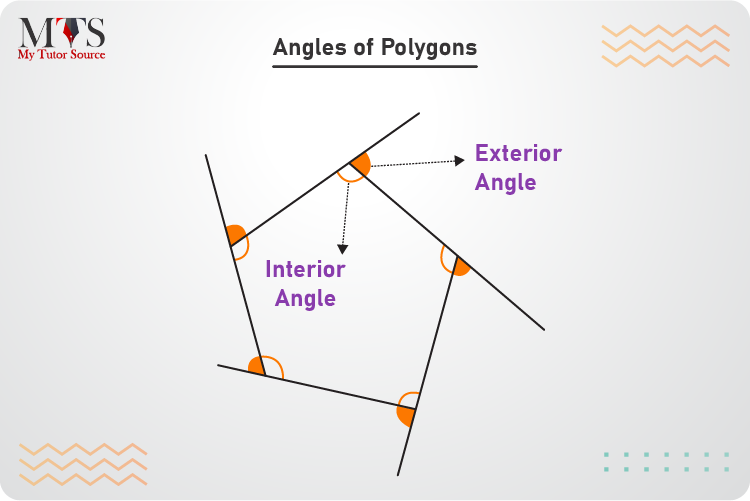
Any of the two given methods calculates the sum of all interior angles of a polygon:
Sum = (n − 2) π radians
n-gon = (n − 2) × 180°
where,
n = number of sides of the polygon
The exterior angles are always formed on the outside of a polygon. By definition, an angle formed by one of the sides of a polygon and the extension of its adjacent side is known as an exterior angle of a polygon.
Note:
Following are the main properties of polygons based on their shapes, sizes, angles, vertices, and types:
You must learn two basic formulas of polygons such as:
The area is the amount of region covered by a polygon in a two-dimensional plane. The formula of the polygon area depends on the type or shape of the polygon.
Units of Area: (meters)2, (centimeters)2, (inches)2, and (feet)2, etc.
Perimeter is the total distance covered by a two-dimensional shape’s sides or boundary length.
Polygon Perimeter = Length of Side 1 + Length of Side 2 + Length of Side 3…+ Length of side N (for an N-sided polygon)
Units of perimeter: meters, cm, inches, feet, etc.
Following are a few polygons with area and perimeter formulas:
Area: ½ x (base) x (height)
Perimeter: a + b + c
Area: side2
Perimeter: 4 (side)
Area: 3√3/2 (side)2
Perimeter: sum of all six sides
Area: ¼ √5(5+2√5) side2
Perimeter: Sum of all five sides
Area: Length x Breadth
Perimeter: 2 (length + breadth)
Area: Base x Height
Perimeter: 2 (Sum of pair of adjacent sides)
Area: ½ (Product of diagonals)
Perimeter: 4 x side
Area: 1/2 (sum of parallel side) height
Perimeter: sum of all sides
Answer: Following are the seven types of polygons:
Solution:
Total number of sides in a signboard = n = 6
Formula of interior angle of polygon = 180º (n-2) / n
Add values in the formula:
Interior angle = (180º (6-2)) / 6
= (720º) /6
= 120º
Hence, each interior angle of the signboard “STOP” measures 120º.
Question 3: How to calculate the diagonals of a polygon?
Answer: The diagonal of a polygon is measured by n (n – 3) /2, where n is the sides of the polygon.
Question 4: How many diagonals does a triangle have?
Answer: Triangles do not have diagonals.
Question 5: The playground of a school is in the shape of an octagon, and the gardener has to place a rope around its perimeter. The sides are 15m, 15m, 8m, 8m, 10m, 10m, 13m, 13m. calculate the total meters of rope the gardener needs for the perimeter?
Solution:
As perimeter is the sum of all sides of a polygon
Required length of rope = perimeter of the playground
Perimeter = 15 + 15 + 8 + 8 + 10 + 10 + 13 + 13
= 92 m
Hence, the total length of the rope required = 92m
Question 6: What does a polygon with 7 sides call?
Answer: 7 sided polygon is called Heptagon, and it has 7 vertices.
Answer: Yes, it is. Star is from the field of geometry, and it is known as a star polygon.
Below is an important table of polygons with their number of sides, vertices, diagonals, and interior angles:
| Polygon | Number of diagonals | Number of vertices | Number of sides | Interior angles |
| Triangle | 0 | 3 | 3 | 60 |
| Pentagon | 5 | 5 | 5 | 108 |
| Hexagon | 9 | 6 | 6 | 120 |
| Heptagon | 14 | 7 | 7 | 128.571 |
| Octagon | 20 | 8 | 8 | 135 |
| Quadrilateral | 2 | 4 | 4 | 90 |
| Nonagon | 27 | 9 | 9 | 140 |
| Decagon | 35 | 10 | 10 | 144 |
| Hendecagon | 44 | 11 | 11 | 147.273 |
| Dodecagon | 54 | 12 | 12 | 150 |
| Triskaidecagon | 65 | 13 | 13 | 158.308 |
| Pentadecagon | 90 | 15 | 15 | 156 |
| Tetrakaidecagon | 77 | 14 | 14 | 154.286 |
We use polygons all day, every day. in fact, in every moment of life in the form of:
