Maths

Trigonometric Ratios – Definition, Formulas, Table and Problems

Chloe Daniel
Published On: March 31 ,2022

Table Of Content

What are Trigonometric Ratios?

Formulas of Trigonometric Ratios

Table of Trigonometric Ratios

Tip to Remember Trigonometric Ratio Formulas

Applications of Trigonometry

Trigonometric Word Problems

Frequently Asked Questions

Scholars worldwide have studied Trigonometry as it is one of the most ancient subjects. Trigonometry deals with measuring triangles’ sides, angles and problems based on them. The word trigonometry is generated from words of the Greek language: trigonon and metron, which means triangle and measure, respectively. It covers a part of mathematics, and learning trigonometric ratios is essential to understand the relationship between angles and sides of a right-angled triangle. Therefore, experienced teachers and private math tutors around the globe conduct lectures on trig ratios.

There are six trigonometric ratios for right-angled triangles with respect to their acute angles. Let us understand the concept of trigonometric ratios with their formulas from the information given below:

What are Trigonometric Ratios?

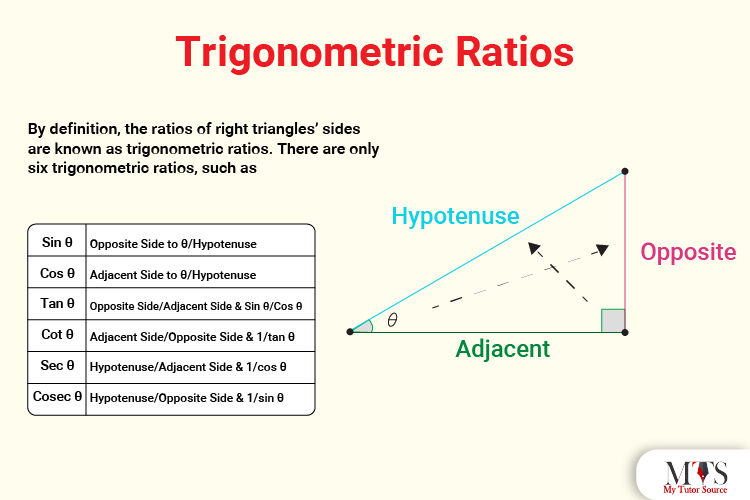
By definition, the ratios of right triangles’ sides are known as trigonometric ratios. There are only six trigonometric ratios, such as

Sine written as Sin
Cosecant written as Cos
Tangent written as Tan
Cosecant written as Cot
Secant written as Sec
Cotangent written as Cosec

Here,

Cosecant or Cot is the multiplicative inverse of Sin or Sine.
Secant or Sec is the multiplicative inverse of Cos or Cosine.
Cotangent or Cosec is the multiplicative inverse of Tan or Tangent.

As triangles have three sides, these ratios are used to find any of the two sides of the given triangle. They are also used to measure the acute angle, θ of the right-angled triangle. All triangles have a

Perpendicular (the side opposite to the angle, θ)
Base (side where right angle stands or adjacent side)
Hypotenuse (longest side of the triangle)

Formulas of Trigonometric Ratios

As per the definition, the perpendicular, hypotenuse and base refer to the lengths of the sides of the right-angled triangle. Go through the table given below to learn the basic formulas of trigonometric ratios:

Trigonometric Ratios Formulas
Sine or sin θ	Perpendicular / Hypotenuse
Cosine or cos θ	Base / Hypotenuse
Tangent or tan θ	Perpendicular / Base
Cotangent or cot θ	Base / Perpendicular
Cosecant or cosec θ	Hypotenuse / Perpendicular
Secant or sec θ	Hypotenuse / Base

Observe the formulas of trigonometric ratios in-depth, and you will determine that all these formulas are somehow generated from each other. For instance, cosine or cos θ is the reciprocal of secant or sec θ.

Following is the table of the new set of trigonometric ratios formulas:

Trigonometric Ratios Formulas
Sine or sin θ	1 / cosec θ
Cosine or cos θ	1 / sec θ
Tangent or tan θ	1 / cot θ
Cotangent or cot θ	1 / tan θ
Cosecant or cosec θ	1 / sin θ
Secant or sec θ	1 / cos θ

Table of Trigonometric Ratios

The standard angles of trigonometric ratios are 0°, 30°, 45°, 60°, and 90°. Using the table given below, calculating values of different angles of trigonometric ratios becomes easy. Students must learn the value of specific angles for quick calculations.

Trigonometric Ratios Sum Identities

sin (A + B) = sin A cos B + cos A sin B
cos (A + B) = cos A cos B – sin A sin B
tan (A + B) = (tan A + tan B) / (1 – tan A tan B)
cot (A + B) = (cot A cot B – 1) / (cot B – cot A)

Trigonometric Ratios Difference Identities

sin (A – B) = sin A cos B – cos A sin B
cos (A – B) = cos A cos B + sin A sin B
tan (A – B) = (tan A – tan B) / (1 + tan A tan B)
cot (A – B) = (cot A cot B + 1) / (cot B – cot A)

Trigonometric Ratios Product Identities

2 sin A * cos B = sin (A + B) + sin (A – B)
2 cos A* cos B = cos (A + B) + cos (A – B)
2 sin A * sin B = cos (A – B) – cos (A + B)

Tip to Remember Trigonometric Ratio Formulas

Tip 1. SOH – CAH – TAO

It is one of the easy ways to learn and memorize formulas and definitions of three trigonometric ratios i.e., sin, cos and tan.
Here,

SOH is for
Sin = Opposite / Hypotenuse

CAH is for
Cos = Adjacent / Hypotenuse

TOA is for
Tan = Opposite / Adjacent

Note: Opposite and Adjacent in the formulas mentioned above refers to Perpendicular and Base, respectively.

Tip 2. Mnemonics

Another exciting yet easy tip to learn and memorize trigonometric ratios is trigonometric mnemonics which is
Some People Have Curly Brown Hair Through Proper Brushing

Here,

Some People Have is used for
Sin = Perpendicular / Hypotenuse

Curly Brown Hair is used for
Cos = Base / Hypotenuse

Through Proper Brushing is used for
Tan = Perpendicular / Base

Applications of Trigonometry

Trigonometry is the branch of math, but its ratios are widely used in architecture, physics, satellite navigation systems and many other calculations. With hands-on expertise in trigonometric ratios finding heights, studying waves, calculating distance and angles is an easy task. Here are a few applications of trigonometry:

Measuring roof slopes and inclination
Measuring a building’s height and width
Measuring fields, ground surfaces and lots
Measuring heights of mountains and towers
Calculating speed, angle, direction and slope
Using radar systems
Finding path, direction and speed of bullets or rocket fired
Finding mechanical and electromagnetic waves (physical quantities)
Finding cross product, waves, circular motions, vector and optics
Surveying
Performing CT scans and ultrasounds
Making oceanography and computer graphics

Trigonometric Word Problems

Question: BOP is a right-angled triangle, at O, hypotenuse BP = 12 units, perpendicular BO = 6 units and base OP = 8 units. Find its trigonometric ratios sin θ, cos θ, and tan θ if ∠BOP = θ.

Solution:

Given that
Perpendicular = 6
Hypotenuse = 12
Base = 8

Trigonometry ratio formulas are
Sin θ = Perpendicular / Hypotenuse
Cos θ = Base / Hypotenuse
Tan θ = Perpendicular / Base

By putting values,
Sin θ = 6 / 12 = 1 / 2
Cos θ = 8 / 12 = 2 / 3
Tan θ = 6 / 8 = 3 / 4

Hence, sin θ, cos θ, and tan θ of a given BOP right-angled triangle are ½, 2/3, and ¾ respectively.

Question: Suppose a man is standing on a building at a distance of 210 ft from point C on the ground. What would be the height of that building id tangent or tan θ = 2/4?

Solution:

Given that
Base = 210
Tan θ = 2/4

As per trigonometry ratio,
Tan θ = Perpendicular / Base

By putting values
2/4 = Perpendicular / 210
Perpendicular = (2 x 210/3) = 105
Here, Perpendicular = Height

Hence, the height of the given building is 105ft only.

Frequently Asked Questions

Write a mnemonic to learn the trigonometric ratios?

SOH-CAH-TOA is one of the easy mnemonics to learn and memorize the three primary trigonometric ratios: sin, cos, and tan.

What are the complementary angles of trigonometry?

A pair of two angles with their sum equal to 900 are known as complementary angles. The complement of an angle is represented as (90° – θ).
Here are the trigonometric ratios of complementary angles:

sin (90°- θ) = cos θ
cos (90°- θ) = sin θ
tan (90°- θ) = cot θ
cot (90°- θ) = tan θ
cosec (90°- θ) = sec θ
sec (90°- θ) = cosec θ

Name all trigonometric ratios:

There are a total six trigonometric ratios named as, sine (sin), cosine (cos), tangent (tan), secant (sec), cotangent (cot), and cosecant (cosec).

Write formulas of sine and cosecant:

The formulas are given below

Sine = Perpendicular / Hypotenuse
Cosecant = Hypotenuse / Perpendicular

Find Top Tutors in Your Area

Find A Tutor

Chloe Daniel

With over 3 years of experience in teaching, Chloe is very deeply connected with the topics that talk about the educational and general aspects of a student's life. Her writing has been very helpful for students to gain a better understanding of their academics and personal well-being. I’m also open to any suggestions that you might have! Please reach out to me at chloedaniel402 [at] gmail.com