Maths

Trigonometry Formulas

Chloe Daniel
Published On: March 30 ,2022

Trigonometry is one of the most important yet difficult branches of mathematics, and you will come across dozens of problems that will need Trigonometry Formulas. But the question is, are you fully familiar with Trigonometric formulas?

If not, then don’t worry. We have got you covered! In this post, we are going to share a detailed and easy-to-understand list of all the Trigonometry formulas, along with identities and functions. But before that, let’s take a brief look at what Trigonometry is. Read on!

What is Trigonometry?

Trigonometry basically studies and deals with the relationship of lengths, angles, and sides of triangles. Moreover, trigonometric functions and formulas are widely used in navigating and surveying systems, geography, and astronomy too!

The most common Trigonometric Functions you will hear are tan (tangent), sin θ (sine), cos θ (cosine), sec θ (secant), cot θ (cotangent), and cosec θ (cosecant). Don’t panic, we will explain these Trigonometric Functions in detail, just try to stick till the end!

List of Trigonometry Formulas

As we have briefly mentioned above, you will need to use Trigonometry formulas to solve hundreds of Mathematics problems. Also, these formulas are only applicable to right-angled triangles.

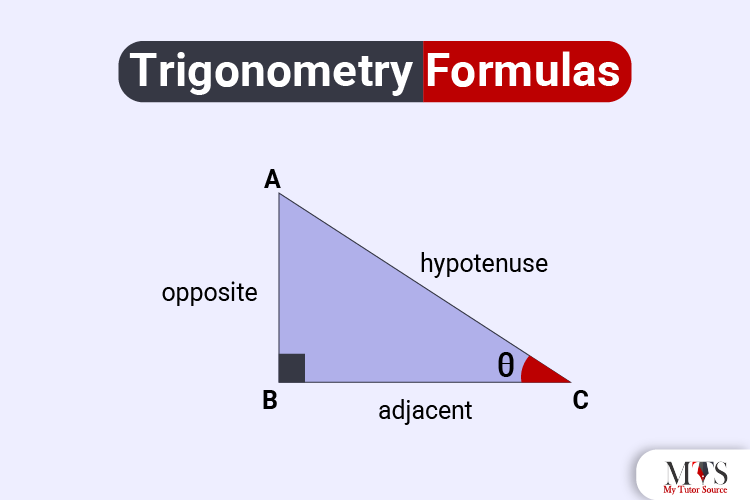
With that being said, we will be mainly working with 3 sides of the right-angled triangle: Perpendicular (Opposite side), Base (Adjacent side), and Hypotenuse.

The Hypotenuse is the longest side, the Perpendicular is the opposite side of the angle, and the base is where both Hypotenuse and Perpendicular rest.

Now without making you wait any further, let us get on with our list of Trigonometry formulas and their detailed explanation:

Basic Trigonometric Formulas

Before diving into the complex ones, let’s go through the basic trigonometry formulas first, also known as Trigonometric functions. There are a total of six trigonometric functions that include sin, cos, tan, sec, cot, and cosec.

Here are the formulas and trigonometric identities of these ratios derived by keeping a right-angled triangle as a reference:

sin θ = Perpendicular (Opposite side) / Hypotenuse
cos θ = Base (Adjacent side) / Hypotenuse
tan θ = Perpendicular (Opposite side) / Base (Adjacent side)
sec θ = Hypotenuse / Base (Adjacent side)
cosec θ = Hypotenuse / Perpendicular (Opposite side)
cot θ = Base (Adjacent side) / Perpendicular (Opposite side)

Reciprocal Identities

The reciprocal trigonometric identities are derived by keeping a right-angled triangle as a reference and using the basic trigonometric ratios. Here is a list of reciprocal identities and their formulas:

sin θ = 1/cosec θ
cos θ = 1/sec θ
tan θ = 1/cot θ
sec θ = 1/cos θ
cot θ = 1/tan θ
cosec θ = 1/sin θ

Trigonometric Ratio Table

We are compiling some of the most commonly used trigonometry formulas and angles you will find in most trigonometric problems. Here it is:

Angles (In Degrees)	0°	30°	45°	60°	90°	180°	270°	360°
Angles (In Radians)	0	π/6	π/4	π/3	π/2	π	3π/2	2π
sin	0	1/2	1√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1
tan	0	1√3	1	√3	∞	0	∞	0
cot	∞	√3	1	1/√3	0	∞	0	∞
cosec	∞	2	√2	2√3	1	∞	-1	∞
sec	1	2√3	√2	2	∞	-1	∞	1

Periodic Identities

The trigonometry formulas for periodic identities are basically used to shift the angles of π, π/2, 2π, etc. Moreover, these periodic and trigonometry identities will keep repeating themselves are short intervals of time. Why? Well, because they are known to be cyclic in nature.

Here are the trigonometry formulas of periodic identities according to different quadrants, and in radians:

First Quadrant

sin (π/2 – θ) = cos θ
cos (π/2 – θ) = sin θ
sin (π/2 + θ) = cos θ
cos (π/2 + θ) = – sin θ

Second Quadrant

sin (3π/2 – θ) = – cos θ
cos (3π/2 – θ) = – sin θ
sin (3π/2 + θ) = – cos θ
cos (3π/2 + θ) = sin θ

Third Quadrant

sin (π – θ) = sin θ
cos (π – θ) = – cos θ
sin (π + θ) = – sin θ
cos (π + θ) = – cos θ

Fourth Quadrant

sin (2π – θ) = – sin θ
cos (2π – θ) = cos θ
sin (2π + θ) = sin θ
cos (2π + θ) = cos θ

Co-Function Identities (In Degrees)

The trigonometry formulas of co-function identities help you identify the relationship between various trigonometry functions. Here is how we present these trigonometry formulas in degrees:

sin(90° − x) = cos x
cos(90° − x) = sin x
tan(90° − x) = cot x
cot(90° − x) = tan x
sec(90° − x) = cosec x
cosec(90° − x) = sec x

Trigonometry Formulas for Sum & Difference Identities

sin(x+y) = sin(x)cos(y)+cos(x)sin(y)
cos(x+y) = cos(x)cos(y)–sin(x)sin(y)
tan(x+y) = (tan x + tan y)/ (1−tan x • tan y)
sin(x–y) = sin(x)cos(y)–cos(x)sin(y)
cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
tan(x−y) = (tan x–tan y)/ (1+tan x • tan y)

Trigonometry Formulas for Double Angle Identities

sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan2 x)]
cos(2x) = cos2(x)–sin2(x) = [(1-tan2 x)/(1+tan2 x)]
cos(2x) = 2cos2(x)−1 = 1–2sin2(x)
tan(2x) = [2tan(x)]/ [1−tan2(x)]
sec (2x) = sec2 x/(2-sec2 x)
csc (2x) = (sec x. csc x)/2

Trigonometry Formulas for Triple Angle Identities

sin 3x = 3sin x – 4sin3x
cos 3x = 4cos3x – 3cos x
tan 3x = [3tanx – tan3x]/[1 – 3tan2x]

Trigonometry Formulas for Half Angle Identities

sin (x/2) = ±√[(1 – cos x)/2]
cos (x/2) = ± √[(1 + cos x)/2]
tan (x/2) = ±√[(1 – cos x)/(1 + cos x)]
or, tan (x/2) = ±√[(1 – cos x)(1 – cos x)/(1 + cos x)(1 – cos x)]
tan (x/2) = ±√[(1 – cos x)2/(1 – cos2x)]
⇒ tan (x/2) = (1 – cos x)/sin x

Inverse Trigonometry Formulas

In these inverse trigonometry formulas, the value of x can be in fractions, decimals, exponents, and whole numbers.

sin-1 (–x) = – sin-1 x
cos-1 (–x) = π – cos-1 x
tan-1 (–x) = – tan-1 x
cosec-1 (–x) = – cosec-1 x
sec-1 (–x) = π – sec-1 x
cot-1 (–x) = π – cot-1 x

Major Systems of Trigonometry Formulas

Maybe you already got an idea about this, but let us explain you thoroughly. All the trigonometric formulas are divided into two major systems. Let us take a brief look on them:

Trigonometric Identities: Trigonometric identities are all the formulas that are linked with Trigonometric functions.

Trigonometric Ratios: Trigonometric ratio is basically the relationship between the side lengths of a right triangle and the measurement of the angles.

Final Words

We tried to explain almost all trigonometric functions, different trigonometric identities, trigonometry ratios, and almost all the formulas in the post above. All of these above formulas will help you solve almost all sorts of trigonometric problems.

Still, if you have any more questions or confusions, feel free to explore our blog and we hope you will surely find your answers!

Frequently Asked Questions

What are the 6 basic trigonometric ratios?

The 6 basic trigonometric ratios are sin, cos, tan, cot, sec, and cosec.

What are the trigonometry formulas for Pythagorean identities?

sin2A + cos2A = 1
1 + tan2A = sec2A
1 + cot2A = cosec2A

Find Top Tutors in Your Area

Find A Tutor

Chloe Daniel

With over 3 years of experience in teaching, Chloe is very deeply connected with the topics that talk about the educational and general aspects of a student's life. Her writing has been very helpful for students to gain a better understanding of their academics and personal well-being. I’m also open to any suggestions that you might have! Please reach out to me at chloedaniel402 [at] gmail.com