Chord of a Circle: Definition, Formula, Theorem & Examples

Learn everything about the chord of a circle along with its terms like chord length formula, chord length, examples using chord length formula, and a lot more. We have designed this blog format for you in an easy-to-understand step-by-step method considering your queries and complexities. Reading this would make you feel like you are reading notes customized by your private math tutor. So, let’s start learning!

What is the Chord of a Circle?

A line segment that connects or joins two points on a circle’s circumference is known as the chord of a circle. By definition, the diameter will be the longest chord of the circle as it passes through the mid or center of the circle, cutting it into two equal halves. Chord’s endpoints will always lie on the circumference of a circle.

Note: circumference is the distance surrounding the circle.

Following is the figure of a circle with the longest chord (diameter) to help you understand the chord of the circle more clearly.

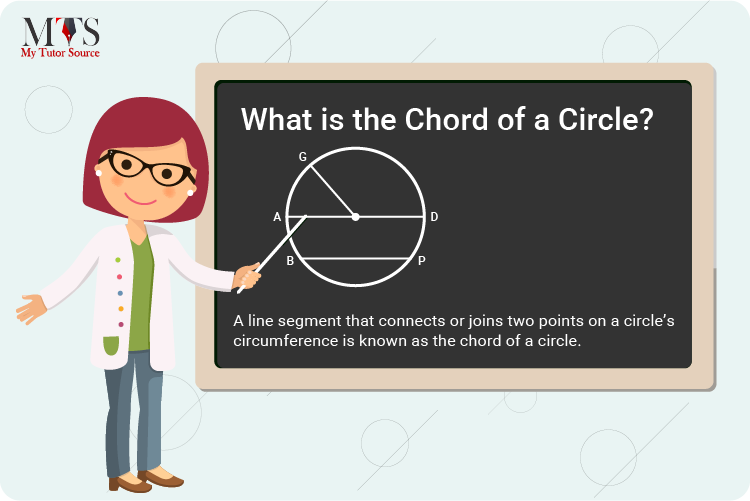
Here, AD represents the circle’s diameter (the longest chord) with ‘O’ as the center. Also, ‘OG’ represents the radius of the circle and ‘BP’ represents a chord of the circle.

Key Parts of a Circle

Before delving into the details, formulas, and questions regarding the chord of the circle, here are the main key parts of a circle. You just need to know:

• Radius: the distance between the circumference of the circle or the center of the circle is called the radius of the circle.
• Diameter: twice the length of the radius of a circle is called the diameter of a circle. It is a line that meets the ends of the circumference of the circle and passes through the center.
• Arc: in the circle, the part of the circumference is known as an arc. A circle has two arcs: major arc and minor arc.
• Major Segment: when a circle is enclosed by a chord and the major arc, its largest part is known as the major segment.
• Minor Segment: when a circle is cut by a chord and the minor arc, its smaller part is known as the minor segment.

Properties of the Chord of a Circle

Following are a few important properties of the chord of a circle, you should know:

1. Only one circle passes through the three collinear points.
2. A chord becomes a secant when it is extended infinitely on both sides.
3. The perpendicular to a chord bisects the chord when drawn from the center of the circle.
4. Chords which are equidistant from the center of the circle have equal length. Or you can say equal chords are equidistant from the center of a circle.
5. The chord of a circle divides the circle into two regions, also known as the segments of the circle: the minor segment and the major segment.
6. Equal chords of a circle have equal angles.
7. If two chords of a circle intersect inside it, then the product of the segment’s lengths of one chord is equal to the lengths of the segments of the other chord.

What is the Chord Length Formula?

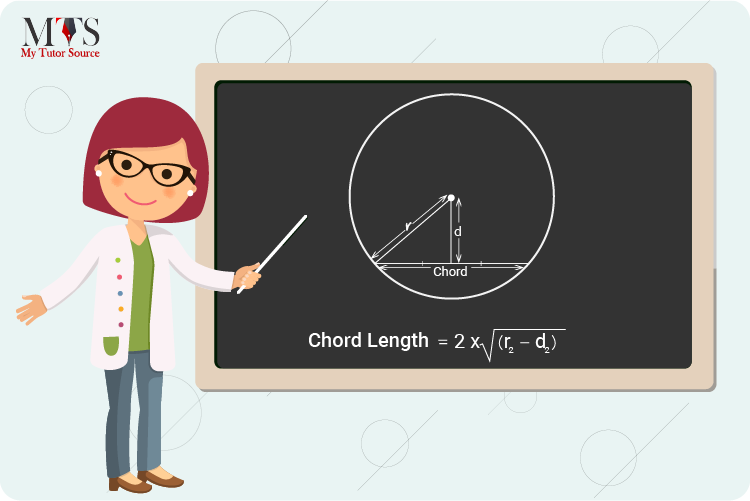
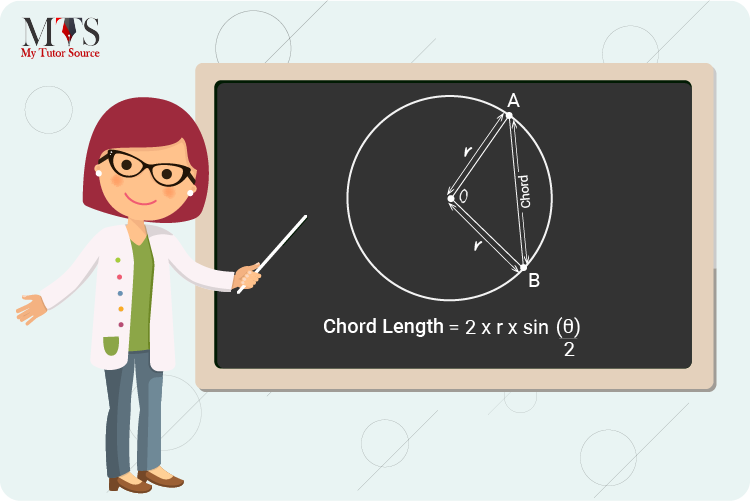
Calculating the length of the chord of any circle is important to solve some questions and theorems related to circles. How to find the chord length of a circle differs as there are two basic formulas for it.

• For calculating the chord length using perpendicular distance from the center, apply:
  Chord Length = Clen = 2 * √ (r2 − d2)

• For calculating the chord length using trigonometry, apply:
  Chord Length = Clen = 2 * r * sin (θ/2)

Here,

r = the radius of a circle
θ = the angle subtended at the center by the chord
d = the perpendicular distance from the chord to the center of a circle

Tip: How to find the right formula to calculate the chord length of a circle?

• If you the radius and the perpendicular distance from the chord to the circle center is given then the formula would be 2 * √ (r2 − d2).

• If you know the value of angle subtended at the center by the chord and the radius of the circle then the formula to find the chord length would be 2 * r * sin (c/2).

Chord Length Formula Example Questions

Question 1: Calculate the radius of the circle if 2 is the perpendicular distance between the chord and the center and 5 is the length of the chord. Use the chord of length formula.

Solution:

Given that,

Length of the chord= Clen = 5
The perpendicular distance between the chord and the center= d = 2
Radius of the circle = r =?
We will find the radius using;
⇒  Clen = 2 * √ (r2 − d2)
(Put given values)
⇒  5 = 2 * √ (r2 − 22)
⇒ 2.5 = √ (r2 − 4)
Now, sqrt on both sides
⇒ 6.25 = r2 − 4
⇒ 6.25 + 4 = r2
⇒ 10.25 = r2
⇒ √ (10.25) = r
⇒ 3.2 = r

Hence, the radius of the circle is about 3.2

Question 2: Jack is eating dinner with his family at a restaurant nearby. He ordered spaghetti for himself, and it was served on a plate of radius 7 inches. What would be the angle swept out the chord if the spaghetti strand is 5 inches long? Apply chord length formula.

Solution:

Formula

Clen = 2 * r * sin (θ/2)

where,

Clen = length of chord = 5

r = radius = 7
(Put values in the formula)

⇒ 5 = 2 x 7 x sin (θ/2)
⇒ 5 = 14 x sin (θ/2)
⇒ 5 / 14 = sin (θ/2)
⇒ sin−1 (5/14) = θ/2
⇒ 0.365 = θ/2
⇒ θ = 0.73

Hence, the angle of spaghetti is 0.73 radians.

Theorems: Chord of a Circle

Theorem 1: Chords with equal lengths subtend equal angles at the center of a circle. Prove equal chords, equal angles of a circle.

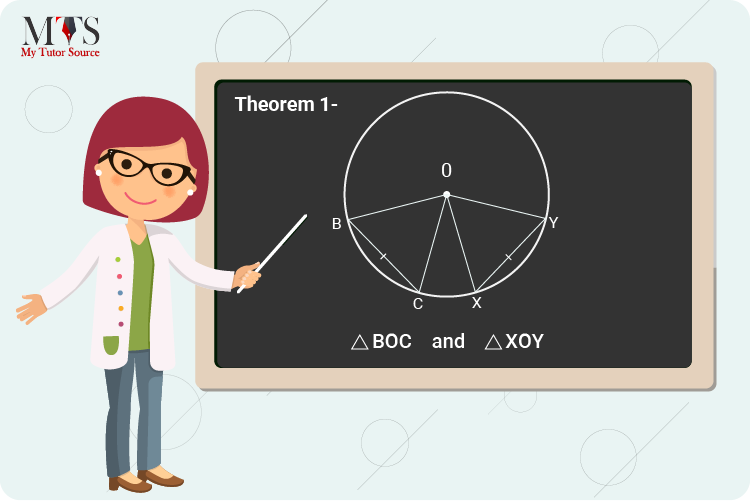
Proof:  ∆BOC and ∆XOY

Given that,

⇒ BC = XY

chords of equal length

⇒ OB = OC = OX = OY

radius of the same circle

⇒ ∆BOC ≅ ∆XOY

side-side-side axiom of the congruence

⇒ ∠ BOC = ∠ XOY

the congruent parts of congruent triangles, CPCT

Hence, proved.

Theorem 2: The measure of angles subtended by the chord at the center of a circle equals the length of the chords. Prove equal angles equal chords.

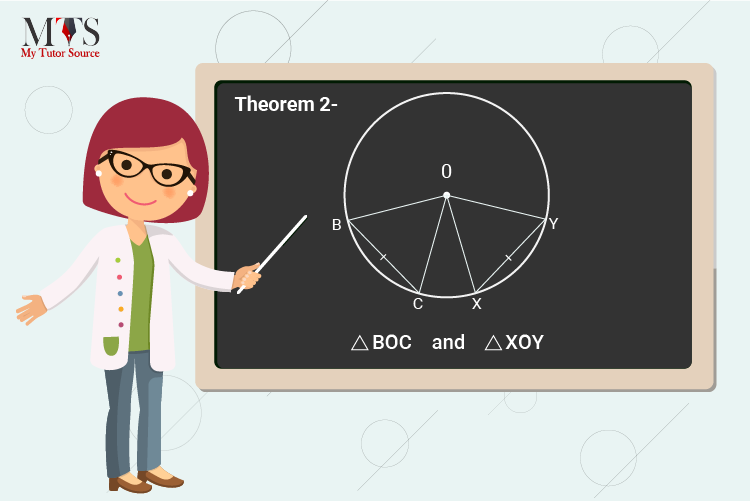
Proof: ∆BOC and ∆XOY

⇒ ∠ BOC = ∠ XOY

given that, equal angles subtend at center O of the circle

⇒ OB = OC = OX = OY

radius of the same circle

⇒ ∆BOC ≅ ∆XOY

SSS or side-side-side axiom of the congruence

⇒ BC = XY

The congruent parts of congruent triangles, CPCT

Hence, proved.

Theorem 3: The perpendicular to a chord, drawn from the center of the circle, bisects the chord. Prove equal chords equidistant from the center of the circle.

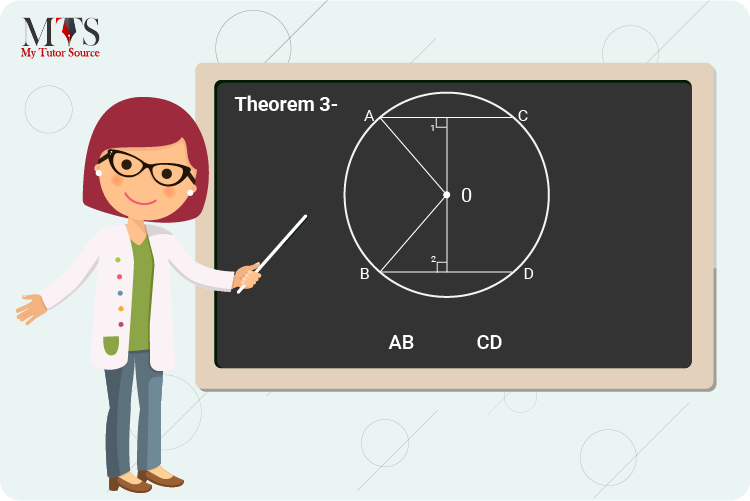
Proof:
Given that, chords AC and BD are equal in length
Now, join A and B with center O and drop perpendiculars from O to the chords AC and BD

⇒ AM = AC/2 and BN = BD/2

These are the perpendicular from the center, bisect the chord

In △OAM and △OBN

⇒ ∠1 = ∠2 = 90°

OM ⊥ AC and ON ⊥ BD

⇒ OA = OB

Radius of the same circle

⇒ OM = ON

Given that

⇒ △OPB ≅ △OND

The RHS Axiom of Congruency

⇒ AM = BN

Two corresponding parts of congruent triangle

⇒ AC = BD

Hence, proved.

Note: We have mentioned the statements and reasons respectively in the theorems.